The computer you’re reading this article on right now runs on a binary — strings of zeros and ones. Without zero, modern electronics wouldn’t exist. Without zero, much of our modern world literally falls apart. Without zero, there’s no calculus, which means no modern engineering or automation.
Humanity’s discovery of zero was “a total game changer … equivalent to us learning language,” says Andreas Nieder, a cognitive scientist at the University of Tüebingen in Germany.
But for the vast majority of our history, humans didn’t understand the number zero. It’s not innate in us. We had to invent it. And we have to keep teaching it to the next generation.
Other animals, like monkeys, have evolved to understand the rudimentary concept of nothing. And scientists just reported that even tiny bee brains can compute zero. But it’s only humans that have seized zero and forged it into a tool.
So let’s not take zero for granted. Nothing is fascinating. Here’s why.
What is zero, anyway?

Our understanding of zero is profound when you consider this fact: We don’t often, or perhaps ever, encounter zero in nature.
Numbers like one, two, and three have a counterpart in the sensory world. We can see one light flash on. We can hear two beeps from a car horn. But zero? It requires us to recognize that the absence of something is a thing in and of itself.
“Zero is in the mind, but not in the sensory world,” Robert Kaplan, a Harvard math professor and an author of a book on zero, says. Even in the empty reaches of space, if you can see stars, it means you’re being bathed in their electromagnetic radiation. In the darkest emptiness, there’s always something. Perhaps a true zero — meaning absolute nothingness — may have existed in the time before the Big Bang. But we can never know.
Nevertheless, zero doesn’t have to exist to be useful. In fact, we can use the concept of zero to derive all the other numbers in the universe.
Kaplan walked me through a thought exercise first described by the mathematician John von Neumann. It’s deceptively simple.
Imagine a box with nothing in it. Mathematicians call this empty box “the empty set.” It’s a physical representation of zero. What’s inside the empty box? Nothing.
Now take another empty box, and place it in the first one.
How many things are in the first box now?
There’s one object in it. Then, put another empty box inside the first two. How many objects does it contain now? Two. And that’s how “we derive all the counting numbers from zero … from nothing,” Kaplan says. This is the basis of our number system. Zero is an abstraction and a reality at the same time. “It’s the nothing that is,” as Kaplan said. (At this point in the story, you may want to take another hit on your bong.)
He then put it in more poetic terms. “Zero stands as the far horizon beckoning us on the way horizons do in paintings,” he says. “It unifies the entire picture. If you look at zero you see nothing. But if you look through it, you see the world. It’s the horizon.”
Once we had zero, we have negative numbers. Zero helps us understand that we can use math to think about things that have no counterpart in a physical lived experience; imaginary numbers don’t exist but are crucial to understanding electrical systems. Zero also helps us understand its antithesis, infinity, in all of its extreme weirdness. (Did you know that one infinity can be larger than another?)
Why zero is so damn useful in math
Zero’s influence on our mathematics today is twofold. One: It’s an important placeholder digit in our number system. Two: It’s a useful number in its own right.
The first uses of zero in human history can be traced back to around 5,000 years ago, to ancient Mesopotamia. There, it was used to represent the absence of a digit in a string of numbers.
Here’s an example of what I mean: Think of the number 103. The zero in this case stands for “there’s nothing in the tens column.” It’s a placeholder, helping us understand that this number is one-hundred and three and not 13.
Okay, you might be thinking, “this is basic.” But the ancient Romans didn’t know this. Do you recall how Romans wrote out their numbers? 103 in Roman numerals is CIII. The number 99 is XCIX. You try adding CIII + XCIX. It’s absurd. Placeholder notation is what allows us to easily add, subtract, and otherwise manipulate numbers. Placeholder notation is what allows us to work out complicated math problems on a sheet of paper.
If zero had remained simply a placeholder digit, it would have been a profound tool on its own. But around 1,500 years ago (or perhaps even earlier), in India, zero became its own number, signifying nothing. In the seventh century, the Indian mathematician Brahmagupta wrote down what’s recognized as the first written description of the arithmetic of zero:
Zero slowly spread across the Middle East before reaching Europe, and the mind of the mathematician Fibonacci in the 1200s, who popularized the “Arabic” numeral system we all use today.
From there, the usefulness of zero exploded. Think of any graph that plots a mathematical function starting at 0,0. This now-ubiquitous method of graphing was only first invented in the 17th century after zero spread to Europe. That century also saw a whole new field of mathematics that depends on zero: calculus.
You may recall from high school or college math that the simplest function in calculus is taking a derivative. A derivative is simply the slope of a line that intersects with a single point on a graph.
To calculate the slope of a single point, you usually need a point of comparison: rise over run. What Isaac Newton and Gottfried Leibniz discovered when they invented calculus is that calculating that slope at a single point involves getting even closer, closer, and closer — but never actually — dividing by zero.
“All infinite processes [in math] pivot around, dance around, the notion of zero,” Robert Kaplan says. Whoa.
Why zero is so profound as a human idea?
We’re not born with an understanding of zero. We have to learn it, and it takes time.
Elizabeth Brannon is a neuroscientist at Duke University who studies how both humans and animals represent numbers in their minds. She explains that even when kids younger than 6 understand that the word “zero” means “nothing,” they still have a hard time grasping the underlying math. “When you ask [a child] which number is smaller, zero or one, they often think of one as the smallest number,” Brannon says. “It’s hard to learn that zero is smaller than one.”
In experiments, Brannon will often play a game with 4-year-olds. She’ll put out a pair of cards on a table or screen. And each card will have a number of objects on it. One card will have two dots, for instance. Another will have three. Here’s an example of what they might see.
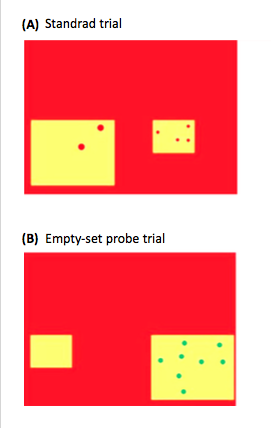
She’ll simply ask the kids to pick the card with the fewest number of objects. When a card with nothing on it is paired with a card with one object on it, less than half the kids will get the answer right.
So what happens to make it all click?
Andreas Nieder, the cognitive scientist from Germany, hypothesizes there are four psychological steps to understand zero, and each step is more cognitively complicated than the one before it.
Many animals can get through the first three steps. But the last stage, the most difficult one, is “reserved for us humans,” Nieder says.
The first is a just having the simple sensory experience of stimulus going on and off. This is the simple ability to notice a light flickering on and off. Or a noise turning on and off.
The second is behavioral understanding. At this stage, not only can animals recognize a lack of a stimulus, they can react to it. When an individual has run out of food, they know to go and find more.
The third stage is recognizing that zero, or an empty container, is a value less than one. This is tricky, though a surprising number of animals, including honey bees and monkeys, can recognize this fact. It’s understanding “that nothing has a quantitative category,” Nieder says.
The fourth stage is taking the absence of a stimulus and treating as it as a symbol and a logical tool to solve problems. No animal outside of humans, he says, “no matter how smart,” understands that zero can be a symbol.
But even well-educated humans can still stumble a bit when thinking about zero. Studies have shown that adults take a few moments longer to recognize the number zero compared to other numerals. And when Brannon’s pick-the-lowest-number-card experiment is repeated with adults, they take slightly longer when deciding between zero and one, than when comparing zero to a larger number.
That suggests that zero, even for adults, takes an extra effort of brain power to process.
What else can understand nothing?

We may not be born with the ability to understand zero. But our capacity to learn it may have deep evolutionary roots, as some new science shows us.
The fourth step in thinking of zero — that is thinking of zero as a symbol — may be unique to humans. But a surprising number of animals can get to step three: recognizing that zero is less than one.
Even bees can do it.
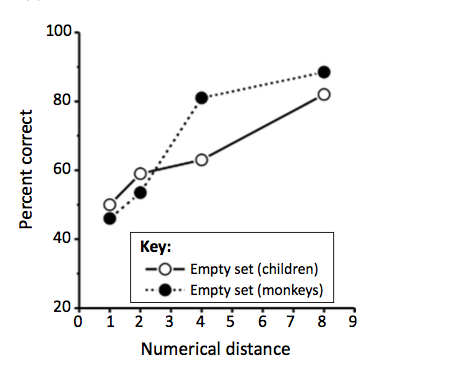
Scarlett Howard, a PhD student at Royal Melbourne Institute of Technology, recently published an experiment in Science that’s almost identical to the one Brannon did with kids. The bees chose the blank page 60 to 70 percent of the time. And they were significantly better at discriminating a large number, like six, from zero, than they were in discriminating one from zero. Just like the kids.
This is impressive, considering that “we’ve got this big mammalian brain but bees have a brain that’s so small weighs less than a milligram,” Howard says. Her research group is hoping to understand how bees do these calculations in their minds, with the goal of one day using those insights to build more efficient computers.
In similar experiments, researchers have shown that monkeys can recognize the empty set (and are often better at it than 4-year-old humans). But the fact that bees can do it is kind of amazing, considering how far they are away from us on the evolutionary trees of life. “The last common ancestor between us and the bees lived about 600 million years ago, which is an eternity in evolutionary times,” Nieder says.
We humans might have only come to understand zero as a number 1,500 years ago. What the experiments on bees and monkeys show us is that it’s not just the work of our ingenuity. It’s also, perhaps, the culminating work of evolution.
There are still great mysteries about zero. For one, Nieder says “we hardly know anything” about how the brain physically processes it. And we don’t know how many animals can grasp the idea of nothing as a quantity.
But what mathematics has clearly shown us is that when we investigate nothing, we’re bound to find something.
Sourse: breakingnews.ie
0.00 (0%) 0 votes